Ha olyan háromszöggel dolgozik, amelyben valahol derékszög van, akkor egyszerűen megtalálhatja az érintőszöget, ha ismeri a háromszög két oldalának hosszát.
Ez még egyszerűbb a Microsoft Excelben, mert vannak beépített függvények, amelyeket használhat.
A cikkben található információk az Excel for Microsoft 365, Excel 2019, 2016, 2013, 2010 és Excel for Mac verziókra vonatkoznak.
Mi az érintőszög?
Az érintőszög egy olyan szög a háromszögben, ahol ismerjük a szöggel ellentétes oldal és a vele szomszédos oldal hosszát.
Például képzelje el, hogy a főnöke azt mondja, hogy a létrát pontosan 70 fokos szögben állítsa a talajhoz képest. Hacsak nem rendelkezik speciális szerszámmal, bonyolult lenne megmérni, hogy a létra és a talaj közötti szög pontosan 70 fokos-e.
Ha azonban van mérőszalagja, meg tudja mérni a távolságot a létra alja és a fal között. Mivel a falhoz támaszkodó létra háromszöget alkot, ez az oldal szomszédos a kiszámítani kívánt érintőszöghöz.
Ezután meg kell mérni a távolságot a fal alja és a létra teteje közötti távolság között. Ez annak az oldalnak a távolsága, amelyik szemközti van az érintőszöggel.
A szemközti és szomszédos oldalak mérésével az arctangens függvény segítségével kiszámíthatja a létra alapjánál bezárt szöget.
Ha a fal (szemközti) oldala 10 láb, a talaj (szomszédos) oldala pedig 5 láb, az érintőszög képlete az ellenkező oldal osztva a szomszédos oldallal. Ez 10 osztva 5-tel, vagy 0,5.
A szög értékének meghatározásához vegye fel a 0,5 arctangensét.
Keresse meg az érintőszöget az Excel segítségével
Találhat olyan számológépet, amely kiszámolja egy érték arktangensét, de az Excelben van egy beépített ATAN függvény, amelyet használhat.
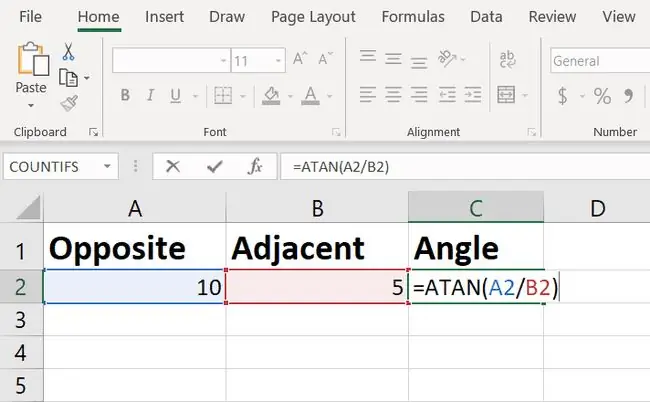
A képlet radiánban adja vissza a szöget, amit a főnöke valószínűleg nem fog megérteni.
A radiánokat át kell konvertálnia fokokra úgy, hogy megszorozza 180/pi-vel. Az Excelnek van egy PI-függvénye is, amelyet erre a célra használhat.
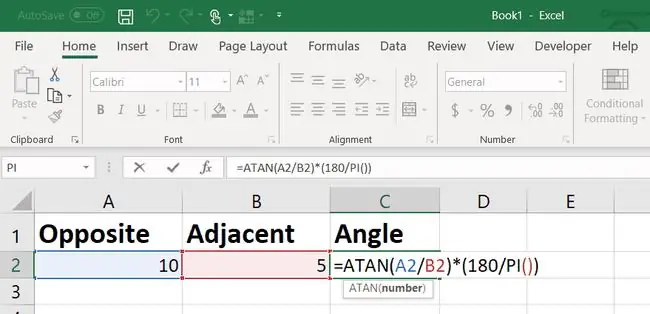
A válasz ebben az esetben 63,43 fok. Ez azt jelenti, hogy az egyik hosszt addig kell beállítania, amíg a szög pontosan 70 fokos lesz.
Ezt egyszerűen megteheti Excelben, mert addig módosíthatja az ellenkező oldal értékét, amíg az arctangens eredménye 70 lesz.
ASIN és ACOS használata Excelben
Ugyanebben a forgatókönyvben tegyük fel, hogy nincs elég hosszú mérőszalagja a fal megméréséhez. Csak azt tudja, hogy a létra 15 lábnyira van, és öt lábnyira van a f altól.
Az Excelnek két másik funkciója is van, amelyek segítségével kiszámíthatja a szöget.
A létra hossza a háromszög hipoténusza, a talajtávolság pedig a szög szomszédos oldala. Mindaddig, amíg a háromszögnek egy derékszögű (90 fokos) szöge van, a birtokában lévő információ határozza meg a használandó képletet.
- Koszinusz: Számítsa ki a koszinuszszöget, ha ismeri a befogó és a szomszédos oldal hosszát.
- Sine: Számítsa ki a szinuszszöget, ha ismeri a befogó és a szemközti oldal hosszát.
Ebben az esetben a szög a szomszédos oldal arckoszinusza osztva a hipotenuzszal.
Mivel tudja, hogy a szomszédos oldal (a talaj távolsága) 5 láb, a létra hossza (hipoténusza) pedig 15 láb, a szög koszinusza 5 osztva 15-tel, vagyis 0,333.
A szög kiszámításához használja az arccosine képletet az Excelben.
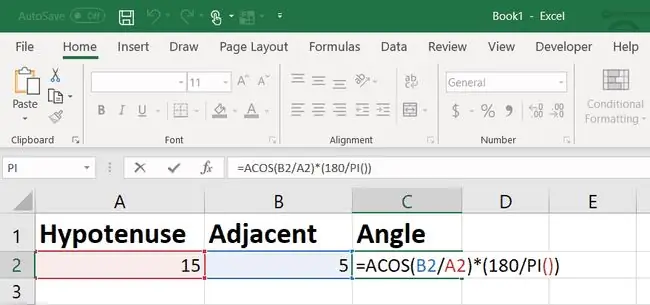
Az arccosine függvény eredménye az, hogy az Excel radiánban van megadva, ezért meg kell szoroznia 180/PI-vel, hogy fokokká konvertálja.
Egy 15 láb hosszú létra esetében, amelynek alapja 5 lábra van a f altól, a szög 70,53 fok.
Ha tudná, hogy a fal magassága (a szemközti oldal) 10 láb, a f altól (a szomszédos old altól) mért talajtávolság helyett az arcszinuszos képletet használná az Excelben.
Ebben az esetben a szög szinusza a szemközti oldal, osztva a hipotenuzszal.
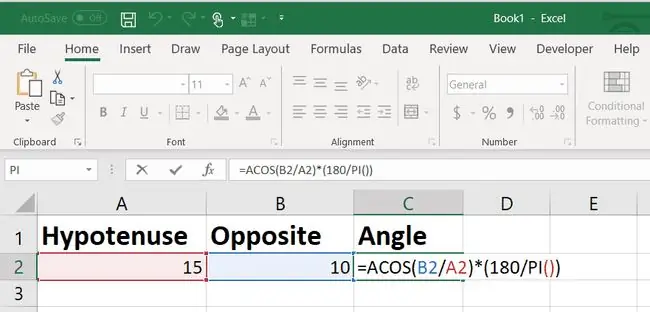
Fokokra konvertálás után a szög ebben az esetben 48,12 fok lenne.
Miért használjunk ATAN-t, ACOS-t vagy ASIN-t?
Íme néhány példa azokra a helyzetekre, amikor szükség lehet az alábbi függvények valamelyikének használatára az Excelben:
- Az asztalos munkákban és az építőiparban a szögeket és a hosszokat minden szempontból alkalmazzák a házak és épületek építésénél.
- A fotósok szögeket használnak a megvilágítás és a kreatív felvételek gondos összehangolására.
- A sportban a szögek megértése javíthatja a készségeket és javíthatja a stratégiát.
- A hajókat és repülőgépeket a radaron szögek és távolságok alapján helyezik el.
- Ha biztos akar lenni abban, hogy a bútorok pontosan illeszkednek a szobájába, tudnia kell, hogyan kell kiszámítani a hosszokat és a szögeket.
Lehet, hogy ezeket a számításokat tudományos számológéppel is elvégezheti. De ha nincs kéznél, az Excel segíthet a számítások elvégzésében.
